はじめに
意図的な論理からの逸脱が「詭弁」、非意図的な論理からの逸脱が「誤謬」です。
論理的に非常に見破り難い詭弁とは、裏を返せば、論理的に非常に誤りやすい誤謬であるということです。
本頁では、難しい詭弁(誤謬)から簡単な詭弁(誤謬)の順に、代表的なものを紹介していきます。
詭弁(誤謬)を見る前に、その準備として正しい推論形式を簡単にまとめます。
正しい三段論法の推論形式は、以下のようになります。
AならばBである
Aである
よってBである運転免許証を取得した人なら、運転ができる
その人は運転免許を取得している
よって、その人は運転ができる
「AならばB」の前に来る仮定Aを「前件」、後ろに来る結果Bを「後件」と言います。
正しい推論は、前件Aを肯定することから後件Bの肯定を導きだすものです。
そのため、前件肯定式(前件肯定-AであるからBである)とも呼ばれます。
ですので、前件Aを否定して後件Bを否定しようとしたり(前件否定-AでないからBでない)、後件Bの肯定から遡行して前件Aを肯定する(後件肯定-BであるからAである)ような逸脱した推論は、誤謬であるということです。
ちなみに後件Bを否定して前件Aを否定するのは(後件否定-BでないならAでない)、正しい推論です(なぜそうなるかは命題論理の頁を参照)。
次いで、正しい選言三段論法の推論形式は、以下のようになります。
選言「または」の入った三段論法です。
AまたはBである
Aでない
よってBである彼は狂人または天才である
彼は狂人でない
よって、彼は天才である
「AまたはB」の選言の一方の否定(選言否定)によって、消去法的に結論を導く方法です。
しかし、反対に「AまたはB」の選言の一方の肯定(選言肯定)によって、正しい結論を導くことは出来ません(後述)。
前件否定の誤謬(詭弁)
「AならばB」の前件Aを否定することで後件Bを否定するという、誤った推論。
AならばBである
Aでない
よってBでない運転免許証を取得した人なら(前件)、運転ができる(後件)
その人は運転免許を取得していない(前件の否定)
よって、その人は運転ができない(後件の否定)
免許証を取得せずとも、私道で練習さえすれば運転ができるようになるので、推論として誤りです。
問題は、AならばBという条件文において、条件Aが満たされない場合のことは何も語られておらず、未規定であるため、Bを導出する別の可能性が残るということです。
後件肯定の誤謬(詭弁)
「AならばB」の後件Bを肯定することで前件Aを肯定するという、誤った推論。
AならばBである
Bである
よってAである運転免許証を取得した人なら(前件)、運転ができる(後件)
その人は運転ができる(後件の肯定)
よって、その人は運転免許を取得している(前件の肯定)
その人は無免許運転の可能性もあるので、この推論は誤りです。
選言肯定の誤謬(詭弁)
選言三段論法における「AまたはB」の一方の肯定(選言肯定)によって、あやまった結論を導く推論です。
AまたはBである
Bである
よってAでない彼は、狂人または天才である
彼は、天才である
よって彼は、狂人でない
天才でありながら狂人である可能性もあるので、この推論は誤りです。
問題は選言「または」の多義性にあります。
合格と不合格のように排他的関係の「または(排他的論理和)」と、天才と狂気のように非排他的な「または(包含的論理和)」があるため、この誤謬が生じます。
選言の否定は、この両方の「または」に妥当するため、どんな状況でも正しい推論になりますが、選言の肯定は、排他的関係の「または(排他的論理和)」においてのみ正しくなります。
例えば、「合格または不合格である。合格である(選言肯定)。よって不合格でない」というように。
性急な一般化
少ない事例や部分的な対象から一般則を導こうとする誤謬が「性急な一般化」と呼ばれるものです。
大阪人Aさんは面白い
大阪人Bさんは面白い
大阪人Cさんは面白い
よって、大阪人はみな面白い
たった三人の事例で性急な判断をくだしています。
もちろん面白くない大阪人も沢山いるので、この推論は誤りです。
これは枚挙的帰納法と同じ形ですが、少ない事例で結論を出す性急さから生ずる誤謬であるという点で、異なります。
言いかえれば、証拠不十分で結論を出す早まった帰納です。
例えば、人類の歴史の無数の死者の事例(十分な証拠)から、「よって、人間はみな死ぬ」という結論を出す場合は、帰納と言えます。
媒概念多義の誤謬(詭弁)
三段論法の大前提と小前提共通に含まれ媒介する概念(媒概念)の多義性によって生ずる誤謬です。
ごはんを一ヶ月間食べずに生きられる人は聖人だ
私はごはんを一ヶ月間食べずに生きた(しかしパンは食べた)
よって、私は聖人だ
大前提の「ごはん」は”食べ物”という意味で、小前提の「ごはん」は”炊いた米”という意味なので、結論「私は聖人だ」は誤りとなります。
字面としては三段論法が繋がって見ますが、意味としては全くつながっておらず、推論として成立していないため、当然結論も誤謬となります。
実際には、上の例のように明確な意味変化であることはなく、概念の曖昧性・多義性を微妙にずらしながら、相手が気付かない内に自分に有利な言論を作る巧妙な詭弁(あるいは気付きにくい誤謬)です。
論点先取と循環論法
根拠の中に既に主張が含まれている時、何か証明しているようで何の証明にもなっておらず、論点先取の誤謬(詭弁)となります。
不正はいけないよ。
人は正しく生きなければならないんだから。君が「人生にお金は必要ない」と言えるのは、君の人生がお金が必要でないものだったからだ。
これが往復的、あるいは円環的に循環する時、循環論法の誤謬(詭弁)となります。
根拠の中に既に主張が含まれ、かつ主張の中に既に根拠が含まれているサイクル状態です。
1.太郎君はいじわるをする
↓
2.なぜそんなことをするかと言うと、太郎君は意地悪な性格だからだ
↓
3.なぜそんな性格になるかと言うと、いじわるをするからだ(1.に戻る)
実際には、上の例のように簡単な構造であることはなく、サイクルが大きく、扱う事柄が多くなるほど、気付くことが難しくなります。
合成の誤謬と分割の誤謬
部分が正しいという事実から、その全体についても正しいと推測するときに生じる詭弁(誤謬)が、合成の誤謬です。
正しいものを合成したら、合成後も正しいものができるとは限りません。
「合成の誤謬」という言葉が、1.正しい部分を合成しても全体としては正しくならないという意味と、2.ある部分の正しさから全体の正しさを推論することが誤りだという意味と、二つの文脈で使われているため、それぞれの例を挙げます。
感染症を流行させないために個々人がマスクをすることは有効だ(部分としては正しい行動)
↓
個々人がマスクを買うと全体として品薄になり、医療従事者や感染者にマスクが渡らず、むしろ感染が増える(全体としては誤った行動となる)分子は命なき物質だ(正しい)
人間は分子で出来ている(正しい)
よって人間は命なき物質だ(誤り)
反対に、全体が正しいという事実から、その部分についても正しいと推測するときに生じる詭弁(誤謬)が、分割の誤謬です。
正しいものを分割したら、分割後も正しいものができるとは限りません。
「分割の誤謬」という言葉が、1.正しい全体を分割しても分割後は正しくならないという意味と、2.ある全体の正しさから部分の正しさを推論することが誤りだという意味と、二つの文脈で使われているため、それぞれの例を挙げます。
某アイドルグループは国民的人気だ。
↓
ソロでも売れると考え解散したら、一年で消えた。三年二組の生徒は超優秀だ(正しい)
鬼塚君は三年二組の生徒だ(正しい)
よって、鬼塚君は超優秀だ(誤り)
誤った二分法と多重質問
両極端な二つの選択肢を提示し、それ以外の選択肢の可能性を見えなくするのが、誤った二分法の詭弁(誤謬)です。
いま高校を辞めたら、一生中卒だぞ。それでも辞めるのか?
この際、通信制や夜間制の学校、高認後大学入学などという選択肢は事前に排除されています。
多重質問とは、質問の中に見えない前提(質問)が隠れており、見える質問に答えると、それがイエスでもノーでも、結局見えない質問に同意(イエス)してしまう詭弁(誤謬)です。
質問の多重性を利用したトリックです。
海外移住するかこの国で我慢するか、君はどちらがよいと考えていますか
どちらを答えても、この国は脱出すべき、あるいは我慢すべき「悪い国」であるという、見えない前提に同意せざるを得なくなるよう仕向けられています(意図的な場合は詭弁、無意識の場合は誤謬として)。
論点すり替え、ストローマン(藁人形)論法
論じている内容と隣接の主題や問題にずらすことにより、気付かれないよう自分の有利な言論を作る詭弁(誤謬)が、論点すり替えです。
先生は「個性を大切にしよう」といつもおっしゃっている。イジメっ子もひとつの個性なので、僕は頑張ってイジメをするんだ。
ストローマン論法とは、反駁が困難な相手の主張の論点をすり替え、さもそれが相手の主張であるかのようにみなし、そのすり替えられた主張(つまり藁人形)を叩くことで議論に勝つ詭弁です(誤読や解釈の歪みの場合は誤謬)。
論点すり替えの限定的(特殊)な使い方です。
花子「イジメは人を傷つけるのでしては駄目だよ」
太郎「人は傷付くことによって成長するんだよ。花子さんは子供の成長を妨げる過保護のママと同じ偽善者だね」
関連性(連想)の誤謬
関連性(連想)の誤謬とは、議論する内容に無関係なものに関連(連想)付け、論敵の意見を弱めたり、自分の意見を強めたりする詭弁(誤謬)です。
多くの場合、まったく論理的でないものに関連(連想)付けられる非常に幼稚な誤謬(詭弁)であるため、簡単に相手も気付きます。
しかし、オーディエンスが多い場合、非常に厄介なものとなります(一般聴衆は印象や感情に流されやすいため)。
これには、相手の過去の行いや人間性やステータスなどに紐づける人身攻撃や、感情に訴えかける論証、権威や人気に訴える論証など、様々なものがあります。
「過去に児童買春で捕まったあなたの教育論など、何の説得力もありませんよ」
「福島の人達の苦しみを知っている人なら、決して原発再稼働なんてバカな考えは出ません」
「ノーベル賞学者の○○さんも、私(一般人)と同じ意見をもっておられます」
この誤謬を三段論法で表すと、
ジョンは悪い人です
ジョンは建物を設計します
よって、その設計は悪いものです
[人格的な不良さと大工として腕は関係がありません]ノーベル賞学者の意見は信頼できる
私(一般人)の意見はノーベル賞学者と同じだ
よって、私の意見は信頼できる
[専門の学問領域において信頼ある意見を発することと、世間一般的な事柄において信頼ある意見を発することは、関係がありません ]
下図のようにAとBに共通する部分を媒介として関連(連想)付け、Aの要素をBに属するものとしたり、Bの要素をAに属するものとしたり、自由に移動させ、自分にとって都合の良い理屈を形成します。
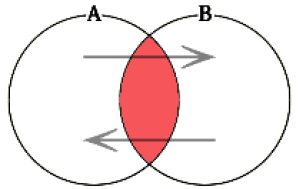
例えば、「人間は動物であり、弱肉強食は必然である。強いライオンが弱い子鹿を捕食するのと同じく、強い人間が弱い人間を餌食にすることは当然の摂理だ」という理屈によって、侵略戦争や奴隷制や資本主義的搾取などを合理化する人達は昔からよく居ます。
この際に為される詭弁は、Aを「ライオン」、Bを「人間」とし、その共通項である「動物(赤い部分)」を媒介にして、ライオンの特性を人間に属するものとして移動させています。
このような詭弁に対しては「人間は肉食獣ではなく、平和的で仲間意識の強い類人猿に属する」と指摘し、カテゴリーの誤謬(詭弁)を明らかにすればよいだけです。
「風が吹けば桶屋が儲かる」的に関連(連想)付けを重ねれば、下図のように簡単に善を悪に貶め、悪を善に偽装することが(詭弁的に)可能です。

「旅行」という概念を基に詭弁の構造を表した図(ショーペンハウアー著、西尾幹二訳『意志と表象としての世界』より)、クリックあるいはタップで拡大
おわりに
ここで紹介したものは、論理的な誤謬を前提とした詭弁術のみです。
論理とは関わりのない手段によって議論に勝つ方法も沢山あります。
私たち一般人の持つ信念や意見は、そのほとんどが論理的に獲得されたものではなく、様々な別の要因によって選択されたものでしかありません。
出木杉君がいくら論理的に真実を述べても、現実に採用されるのはジャイアンの強弁術による(偽の)真実です。
また、詭弁と論理は表裏一体であり、数学や形式論理学の記号のような極端に抽象化されたものを除き、論理は常に詭弁(誤謬)と共に在ります。
それは程度の問題です。
詭弁(誤謬)が或るラインを超えると、論理が生産的な機能を失うため、問題として浮き上がってくるのです。
ここで述べたすべての詭弁は、突き詰めて考えると、論理と溶け合い、区別がつかなくなります。
詭弁を学ぶということは、論理の条件を裏側から学ぶということにほかなりません。
おわり

