第四章、命題論理
一節、命題と真理値(真偽)
先述のように、「命題」とは、真偽を問うことのできる主張をなす文のことです。
命題内容と、それに対応する現実を照合した時に、合っている(事実通りである)ものを「真」、合っていない(事実と反する)ものを「偽」といいます。
命題は真偽を問うことのできる平叙文の形を取り、真偽を問うことのできない疑問文や命令文などの形を取ることはありません。
勿論、平叙文であっても真偽を問うことのできない無意味な文は命題となりません。
・日本の首都は東京である。[真である命題]
・日本の首都は京都である。[偽である命題]
・日本の首都を京都にしろ![真偽を問えないため命題でない]
・日本の首都は京都?[真偽を問えないため命題でない]
・日本と首都へ東京である。[真偽を問えないため命題でない]
命題が真である場合は「1(あるいはT)」、偽である場合は「0(あるいはF、⊥)」と記し、これを「真理値(論理値)」と呼び、第五節の図のような真理値表として表されます。
「日本の京都は美しい」というような、真偽の判断に主観が多く混ざるものは、基本(教科書)的に扱いません。
二節、要素命題と複合命題
「諸星あたるは男である」のように、命題としてそれ以上分割不可能なものを、「要素命題(あるいは単純命題、原子命題など)」といい、「藤波竜之介は男か女である」というような分割可能な命題を、「複合命題(あるいは合成命題、分子命題など)」といいます。
「諸星あたるは男である」を分割すれば、「諸星あたる」「男である」となり、真偽の判断が不可能なものとなり、命題たりえません。
「藤波竜之介は男か女である」は、「藤波竜之介は男である」と「藤波竜之介は女である」という二つの命題を構成要素(要素命題)とする複合的(分割可能)なもので、正確には「藤波竜之介は男である、または藤波竜之介は女である」とあらわすことができます。
三節、命題論理
論理学の主な目的は、推論の正しさ(いわゆる妥当性)の研究です。
「命題論理」は、命題の真偽を形式的に扱い、命題の関係付けにおいてどのように真偽の判定が可能かを明らかにし、その推論の妥当性を保証しようとするものです。
与えられた命題を要素命題に分割し、それを接続詞(論理記号、あるいは論理演算子、論理結合子などとも呼ぶ)で結合されたものとみなし、要素命題の真偽の条件から、その命題全体の真偽を判定する筋道を明らかにする作業です。
ある命題の真偽を導出するために、それを記号論理学に基づく論理式にし、真の値と偽の値の二値によって行う演算が「論理演算」です。
四節、論理記号(論理演算子)と命題記号
論理演算に用いられる基本的な五つの論理記号(論理演算子)は、「否定」「連言」「選言」「条件法」「双条件法」であり、命題論理の対象となる命題は、この五つの論理演算によって作られた複合命題となります。
また、命題自体も形式化され、命題記号として表されます。
以上、命題論理における形式的語彙は次のようなものとなります。
【論理記号】
∧ and かつ 論理積(連言)
∨ or または 論理和(選言)
⇒ if…then…ならば 含意(条件法)
¬ not でない 否定
⇔ 同値(双条件法)【命題記号(命題変項)】
P,Q,R,・・・(任意のアルファベット)【命題記号(命題定項)】
T true 真(恒に)
⊥ false 偽(恒に)
※括弧の略記…論理式における括弧()は、論理記号と命題記号との結び付きの強さに準じ省略可能です。命題記号と最も強く結びつく論理記号が「¬」、次いで「∧ ∨」、次いで「⇒ ⇔」となります。例えば、上の後件否定式((A→B)∧(¬B))→(¬A)であれば、((A→B)∧¬B)→¬Aと省略して記述可能ですが、A→B∧¬B→¬Aと省略してしまえば(A→B)∧(¬B→¬A)という異なるものになってしまいます。
五節、各記号の真理値
・命題定項Tは、真(true)の真理値を常に持つ。
・命題定項⊥は、偽(false)の真理値を常に持つ。
・命題変項P(アルファベットの大文字)は、真(true)あるいは偽(false)を真理値とする変項である。
・P∧Qが真(true)であるのは、Pが真(true)でかつQが真(true)である時に限る。
・P∨Qが真(true)であるのは、Pが真(true)である又はQが真(true)である時 (両方真である場合含む) に限る。
・¬Pが真 (true) であるのは、Pが偽 (false) である時に限る。
・P⇒Qが真(true)であるのは、Pが真(true)であればQも真 (true)である時(⇔非PまたはQ)に限る。
・P⇔Qが真(true)であるのは、PとQが同じ真理値である時に限る。
以上をまとめると、下の図のようになります(真理値表の1は真、0は偽)。

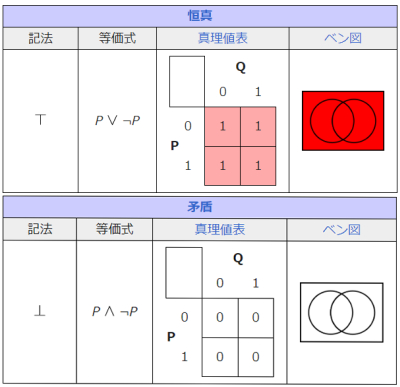
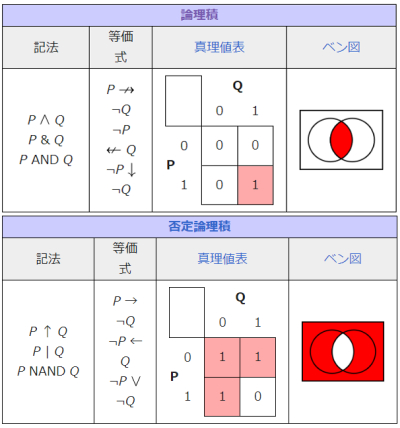


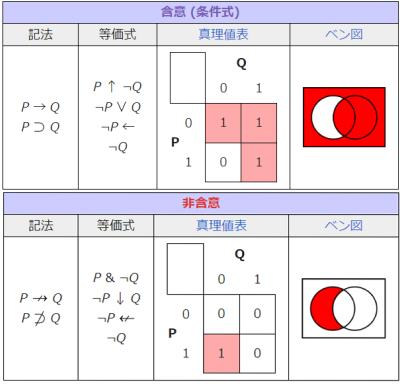
(wikipediaより図版転載2023.05.05時点 )。
六節、真理値の複合
複雑な論理式の真理値は、これらの組み合わせによって、導出することが可能です。
例えば、P∧Q⇒¬P(PかつQならばPでない)は、下図のようになります。
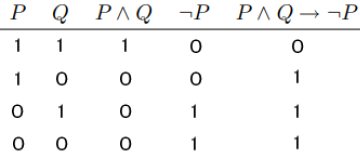
上から一段目を見てみます。
PとQが共に真(1)である時、P∧Qは真(1)です。[五節の図、論理積を参照]
Pが真(1)である時、¬Pは偽(0)です。[五節の図、否定を参照]
前件P∧Qが真(1)で、後件¬Pが偽(0)である場合、条件法(⇒)の論理式は偽(0)となります。[五節の図、含意を参照]
このようにして、論理式の真理値が複合的に導かれます。
七節、恒真式(トートロジー)
命題変項がどのような真理値をとろうと、恒に真となる論理式を「恒真式」あるいは「トートロジー(同語反復)」といいます。
例えば、P∨¬P(Pまたは非P)などです。
この場合、Pが真である時¬Pは偽であり、論理和(∨)の片方が真でもう片方が偽である時は真となります。[五節の図、論理和を参照]
Pが偽である時は¬Pは真であり、論理和(∨)の片方が偽でもう片方が真である時は真となります。[五節の図、論理和を参照]
つまり、命題変項Pがいかなる真理値をとろうと、この論理式全体は常に真となる、トートロジーとなります。
同様に、恒真式である前件肯定式 ((P⇒Q)∧P)⇒Qの真理値を求めると、以下の図のようになります。
八節、正しい推論の判定(意味論的方法)
妥当な推論を判定する方法には、論理式と真理値表によって判断する「意味論-セマンティクス-的方法」と、論理式だけから証明する「構文論-シンタクス-的方法」があります。
意味論的方法は、以下のようなものとなります。
推論とは、「前提P、前提Q、ならば結論R」というような、諸前提(諸仮定)から結論を導く命題のことです。
正しい推論の規準は、「前提がすべて真である時に、必ず結論も真であるもの」です。
ですから、まず自然言語(日常的に使う言葉)から論理式を抽出(形式化)し、さらにその論理式の真理値表を作り、前提が全て真である全ての行で結論が全て真となっていれば、それは妥当な推論だと判定できます。
例えば、前件肯定の三段論法は、以下のように前提を二つ取る推論です。
前提1、PならばQ
前提2、Pである
結論、よって(ならば)Qである
そして、この推論全体の論理式(推論式)は、前提を∧で結び、結論を⇒でつなげて作ることができます。
((P⇒Q)∧P)⇒Q
これは先ほど図で挙げた前件肯定式で、前提の部分を丸(正円)、結論の部分を四角で囲むと、下の図のようになります。
前提○が全て真(1)の行で結論□も真(1)となっており、この推論は「正しい(妥当な)推論である」と判定できます。
推論によっては、前提が全て真(1)の行が複数ある場合があり、その際は、結論も該当する全ての行で真(1)でなければ妥当な推論となりません。
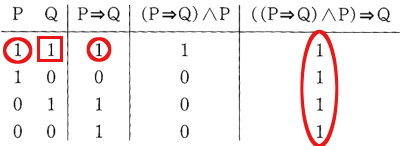
楕円で囲った部分は、この推論全体の論理式(推論式)の真理値ですが、全て真(つまり恒真式)となっています。
前提がすべて真である時に必ず結論も真である推論式は、同時に恒真式でもあるので、真理値表の「丸+四角」の部分でも「楕円」の部分でも、どちらからでも妥当な推論を判定できます。
上図の前件肯定式は、「前提がすべて真である時に必ず結論も真である」「論理式全体が恒真式である」正しい推論であるのに対し、下図のように、後件肯定式 ((P⇒Q)∧Q)⇒P は誤謬を含む推論となります。
赤線で囲った部分を見ていただければ、偽(0)が含まれていてはいけない部分に偽が含まれており、誤った推論であることが判明します。

完全な真理値表を作ることなく、背理法(前頁参照)を用いることによって、推論の妥当性(正しさ)を証明する方法もあります。
反例、つまり「前提がすべて真である時に結論が偽になる」状況(反例モデル)を仮定すると、矛盾が導かれることを示すことによって、逆照射的に元の推論の妥当性を保証します。
正しいとは、裏を返せば「間違いのないこと」を指しているからです。
例えば、仮言三段論法(前頁の推移律のこと)「PならばQ、QならばR、よってPならばR」の場合。
((P⇒Q)∧(Q⇒R))⇒(P⇒R)
前提1、P⇒Q=1
前提2、Q⇒R=1
結論、P⇒R=0
という反例モデル(前提が真で結論が偽)として仮定すると、
結論、P⇒R=0の、Pは1、Rは0になります。[下表は、五節の含意の真理値表を見やすくしたもの]
前提1、P⇒Q=1のPに上で導かれた1を入力すると、Qは必然的に1になります。
前提2、Q⇒R=1のQに上で導かれた1を入力すると、Rは必然的に1になります。
すると、Rは1(真)でもあり0(偽)でもあるという矛盾が生じ、この反例モデルが間違いであることが判明し、仮言三段論法の推論が妥当であることが明らかになります。
九節、正しい推論の判定(構文論的方法)
「構文論(証明論)的方法」は、真理値ではなく、推論の式だけから、その推論の妥当性を証明する方法です。
目の前にある正誤不明な複雑な推論を、既知の確実な推論へと分解(分析)し、理解(証明)することです。
正しいと分かっている基本的で単純な推論を総合したものなら、その正誤不明な推論も確実に正しいはずだからです。
無数にある妥当な推論のなかから、基本的な類型となるようなものを抽出したものが「推論規則」であり、与えられた推論がこの推論規則の積み重ねで構成されていることを示すことができれば、その推論の妥当性を証明することができます。
「証明」とは、与えられた仮定や前提が結論を導く「こうこうである(前提)ならば⇒こうこうなる(結果)」という複雑な推論の、前提と結果の間(⇒)を、単純で確実な推論の積み重ね(推論規則)で埋めることによって、その複雑な推論の妥当性(正しさ)を明らかにする作業です。
この前提から結果へ進む単純な推論のステップを規定するものが「推論規則」であり、推論規則を組み合わせ用いることによって、前提となる式を変形し別の式を導き出し、最終的に結論に至ります(その正誤不明な推論が妥当な推論である限りにおいて)。
推論規則
規則1「含意の導入則」…Pを仮定してQがみちびかれる時、P⇒Qを導出できる。[⇒I]
規則2「含意の除去則(前件肯定式)」…P⇒QとPから、Qを導出できる。[⇒E]
規則3「否定の導入則」…Pから⊥(矛盾)が導かれる時、¬Pを導出できる。[¬I]
規則4「否定の除去則」…¬PとPから、⊥を導出できる。[¬E]
規則5「論理積の導入則」…PとQから、P∧Qを導出できる。[∧I]
規則6「論理積の除去則」…P∧Qから、Pを導出できる。P∧Qから、Qを導出できる。[∧E]
規則7「論理和の導入則」…Pから、P∨Qを導出できる。Qから、P∨Qを導出できる。[∨I]
規則8「論理和の除去則」…P∨QとP⇒R、Q⇒Rから、Rを導出できる。[∨E]
規則9「矛盾の除去則」…⊥から、任意の論理式Pを導出できる。[⊥E]
規則10「二重否定の除去則)」…¬¬Pから、Pを導出できる。[¬¬E]
規則11「背理法」…¬Pから、⊥が導かれる時、Pを導出できる。[RAA]※導入則はInduction(導入)の頭文字の”I”、除去則はEliminatio(除去)の頭文字の”E”を取って、いかなる推論規則が使われたかの識別子として示されます。例えば、含意の除去がなされたなら「⇒E」、論理積の導入がなされたなら「∧I」となります。
※推論規則をいかなるものとするかはある程度任意であり、目的によって異なります。ここで挙げたものはゲンツェンの自然演繹体系に拠るものです。
証明の記述には、論理式の列によるものと、演繹図によるものがあります。
例えば、三段論法((P⇒Q)∧P)⇒Qを論理式で証明する場合は、
1 P⇒Q (前提)
2 P (前提)
3 Q (1,2より)
演繹図(ここではNK演繹図)を使用する場合は、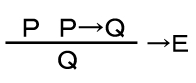
という形になります。
演繹図では、長い横線の上に条件となる式を並べ、横線の右に使用した推論規則の種類を示し、横線の下に導出される結論の式を書きます。
階段を下りていくようにこれを繰り返し、証明すべく与えられた推論の結論が、一番下に導出されます。
例えば、「前提P∧Q、前提P⇒(Q⇒R)、結論R」の推論の証明の場合、以下のようになります。
(佐々木昭則/弓削隆一著『例解 論理学入門』ミネルヴァ書房、29頁図)
