序章、論理学と推論
「論理学」とは、古代ギリシャの哲学者アリストテレスが、真なる認識を得るために考案した体系的方法です。
後に数学的により形式化され、「記号論理学」となります。
その内、特にアリストテレス論理学に沿う古典的なものが「命題論理」「述語論理」であり、これが一般的な知識として必要とされる論理学です。
論理的推論の方法には、「帰納法」と「演繹法」があります。
帰納法とは、複数の個々の事実(事例)から一般法則を導出する(上りの)方法で、演繹法とは、一般法則から個々の事実を求める(下りの)方法です。
有名なプラトンのイデア論やディアレクティケー(弁証法)は、帰納法の色合いが強く、事物の本質(いわゆるイデア)や一般法則を抽出する作業を主な目的とします。
その弟子のアリストテレスの論理学は、主に演繹法を扱い、一般法則から個々の事実を導出する際の正確さを追究する学問です。
帰納法は、「太郎は死んだ、花子は死んだ、マイケルは死んだ、・・・」という複数の事実から、「人間は死ぬものである」という人間の本質や一般法則を抽出する作業です。
勿論、人類誕生からの全人間(推定1080億人)の死亡を確認する完全枚挙ではないので、蓋然的な真理です。
演繹法とは、その「人間は死ぬものである」という一般法則から、「キアヌ・リーブスは人間である、よってキアヌ・リーブスは死ぬものである」という事実を導出する作業です。
演繹が生じた歴史的文脈や動機を無視して、一般的に演繹を定義付ければ、「前提が真であるなら結果も必ず真であるような推論」です。
なにも普遍的な法則から個別事例を導く手続きに限る必要はありません。
帰納法やアブダクション(演繹の遡行)のような推論は、蓋然的なものであるのに対し、演繹的推論は必然的に真を導くものであり、その性質から演繹の「真理保存性」などとも言われます。
ですから、本質的な意味では「推論」は演繹を指し、帰納やアブダクションは「推測」と言った方がよいかもしれません。
勿論、厳密に言えば、演繹の前提も蓋然的に真であるにすぎません(例えば「地球は丸い」も「人間は死ぬ」も、帰納法によって抽出された蓋然的な真です)。
そうではなく、真理保存性とは、その前提を真であると(便宜的に)認めたなら、結論も確実に真であるという、形式的な、推論過程の(必然的)確実性を指しています。
例えば、「石は死ぬものである。ターコイズは石である。よってターコイズは死ぬものである」は、現実との照合(真理値-後述-)としては偽であっても、演繹としては正しいということです。
第一章、論理とは何か
私たちは言葉を話したり物を考える時、短い言葉をつなげて、非常に長い言葉のつながり(関係付け)を作ります。
そして、この言葉のつながりは、多くの場合、演繹的推論を隠れた規則として、成立しています。
日常生活においては、言葉のつながりは大体で良いのですが、状況により、この長い言葉のつながりの正確性(妥当性)が求められることがあります。
この大体を許さない正確な言葉のつながり(関係付け)の状態が、論理的であるということです。
経営者や裁判官や学者のように、常に考えの真偽を問われる立場にある人は、言葉のつながりの正確さを生じさせる原理を明確にし、よく理解しておく必要があります。
そして、その正確に言葉をつなぐ原理を明らかにするものが、論理学です。
論理学において重要なことは、”つながりの正確さ”を求めることであり、文の描写内容自体の正確さ(現実との照合)を探究するものではありません。
現実の論証においては、描写内容自体の正しさと、論理的なつながりの正しさの、二つの正しさが必須になるわけですが、論理学は主に後者の正しさに関わるものです。
正確な言葉のつながりとは、いわば当たり前のことを述べるにすぎませんが(人間はみな死ぬ、太郎は人間だ、よって太郎は死ぬ)、このつながりが長くなると、思いもよらなかったもの、今まで見えていなかったものが発見されます。
例えば名探偵は、将棋の棋士のように、一般の人より遥かに長い言葉のつながり(論理)を頭の中で構築することが出来る為、泥棒に入られた部屋の些細な痕跡から、犯人を推論することが出来ます。
このように、いま現在見えていないものを、言葉のつながりによって導出することを「推論」といいますが、論理学は主にこの推論(演繹的推論)を中心に考える学問です。
演繹的推論とは、演繹の前提の中に含まれている情報を展開する作業であるため、必然的に正しくならざるをえない(真理保存性)のです。
つまり、演繹の結論においては、前提で述べられたこと以上の情報は何も語られておらず、気付いていなかった事に気付かせるだけにすぎません。
先ずは、小さいつながりである、「ない」「かつ」「または」「ならば」を解説し、その後、大きなつながりである「命題論理」に入ります。
命題論理の拡張である「述語論理」では、「すべて(全称)」「ある(存在)」を扱います。
以上の六つの語彙で記号論理学は成り立っています。
混乱しないよう、先に使用する語彙を整理しておきます。
∧ and かつ 論理積 連言
∨ or または 論理和 選言
⇒ if…then…ならば 論理包含 含意
¬ not でない 否定
⇔ 同値
第二章、否定「~ない」
一節、反対概念
言葉と言葉のつながりの一つとして、「~ない」という否定の関係があります。
「~」に入る言葉と違っている場合に、使われます。
例えば、「リンゴがない」「赤色でない」という場合、否定は必ず否定する前の肯定の言葉(「リンゴがある」「赤色である」)を前提にしている関係的なもので、否定は自立的には存在できません。
ここで注意しなければならないことは、「否定」は「反対概念」ではないということです。
例えば、「熱い」の否定は「熱くない」であり、熱いの反対概念は「冷たい」です。
「リンゴ」や「赤色」には、反対概念がないので、分かりやすいのですが、反対概念がある言葉の場合、否定と反対概念が混同され、誤りが生じます。
例えば、健康の為に常温の飲料を好み、飲食店員に「熱くない」お茶をくださいと言えば、かなりの確率でコップが結露したような「冷たい」お茶を持ってきます。
「熱くない」とは、熱い状態以外のものすべてを含むため、さらに「冷たい」も否定した上で、「熱くも冷たくもないお茶をください」と言わなければ、正しく(つまり、論理-言葉のつながりの正確さ-的に)伝わりません。
二節、排中律
伝統的な論理学においては、この肯定と否定の関係を、肯定「である」か、否定「でない」かの、あれかこれかのどちらか一方しか成り立たないものとします。
この論理学の基本的な規則を「排中律(Law of excluded middle)」と言います。
中間(middle)を排除(excluded)する規則(Law)で、「排中律」です。
例えば、「熱くあり、かつ熱くないお茶」というのは、論理的に矛盾しています。
下のベン図のように、隙間なく肯定(P)と否定(notP)の間で重なる部分がない状態が排中律です。
重なる部分が無いということは、「かつ」でくくれる共通の部分が無いということです。
ですから、PとnotPを「かつ」でくくろうとする矛盾は、何も指していない空虚なものとなります。
肯定「Pである」
否定「Pでない」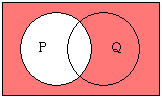
矛盾「Pである、かつPでない」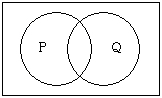
三節、二重否定律
この排中律を規則とした場合、二重否定(否定の否定)=肯定となり、これを「二重否定律(Law of double negation)」と言います。
例えば、「リンゴは果物である」⇔「<リンゴは果物でない>ではない」。
両矢印⇔は「同値」の記号で、一方の命題が真の場合もう一方も必ず真になり、一方の命題が偽の場合もう一方も必ず偽になる際に使われます。
「not(notP)はPに等しい(同値)」、より記号化すると「¬¬P⇔P」と書きます。
もし、「Pの否定の否定」が「Pの肯定」にならないなら、「Pの否定」と「Pの肯定」の間に中間状態が存在することになり、排中律が破綻することになります。
つまり、排中律と二重否定律は、同じ規則を別の側面から見たものです。
※「命題」とは、真偽の性質をもち、真偽の判断の対象となりうる言葉(文章)のことです。例えば、単なる「リンゴ」という言葉は、真偽の判断が不可能なので命題ではありませんが、「リンゴは果物である」は、真偽を問うことが出来るので、命題です。また、大文字のアルファベット(AとかPとか)は、任意の命題を表現しています。
四節、矛盾律
論理的な基本的規則である排中律が破綻した「Pである、かつPでない(熱くあり、かつ熱くないお茶)」ような状態を、「矛盾」と言います。
形式的に書くと「PかつnotP」、より記号化して「P∧¬P」。
両立不可能(排中律)なはずのものが、両立してしまっている状態です。
そして、この矛盾はいけないよ、という規則を、「矛盾律」と言います。
矛盾律は「<Pである、かつPでない>でない」となり、記号化すると「¬(P∧¬P)」と書きます。
※「矛盾律(Law of contradiction)」という語は、その語意から誤解を招きやすいので、「無矛盾律(Law of noncontradiction)」とも言います。ややこしいですが、「矛盾律」=「無矛盾律」です。
五節、背理法
これら、排中律、二重否定律、矛盾律の三つを総動員した間接的な論証を「背理法」と言います。
命題Pを証明する際に、命題Pが偽であると仮定すると矛盾が生じてしまうことを示すことによって、命題Pが真であることを、間接的に証明する方法です。
「リンゴは果物である」という命題を、背理法によって間接論証したい場合は、「リンゴは果物でない」という命題を仮定し、この仮定された命題から矛盾を導出すれば、「リンゴは果物である」を逆サイドから証明することが出来ます。
第三章、接続「かつ」「または」「ならば」
一節、接続
言葉のつながり(関係付け)において、否定と並ぶ重要なものとして、接続があります。
私たちが普段使う様々な接続詞から、その元となっている基本的な型を抽出すると、「かつ(and)」「または(or)」「ならば(if,then)」となります。
二節、「かつ(and)」
「PかつQ」とは、PとQの両方が同時に正しいものとして成立している状態です。
「論理積」や「連言」などと呼ばれます。
論理積「PかつQ」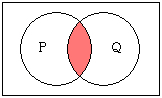
三節、「または(or)」
「PまたはQ」とは、少なくともPとQの片方が正しいものとして成立している状態です。
「論理和」や「選言」などと呼ばれます。
注意しなければならないのは、普段私たちが使う「または」は、「PとQいずれか一方のみが成り立ち、もう一方は成り立たない(排他的論理和、排反的選言)」という意味合いが強いのですが、論理学における「または」は、「PとQの最低どちらか一方は成り立つ(包含的論理和、両立的選言)」というものです(つまり両方が正しいこともありうる)。
選言「PまたはQ」の一方の”不成立”を確認すれば、消去法的にもう一方の成立を証明することができますが、一方の”成立”を確認しても、もう一方が成立/不成立どちらになるかは分からないということです。
[詳細は、選言肯定の誤謬の項をご覧ください。]
論理和(包含的)「PまたはQ」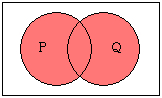
論理和(排他的)「PまたはQ」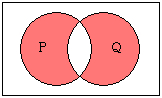
四節、「ならば(if…then…)」
「PならばQ」とは、Pを仮定した時にQが導かれる状態で、これを「条件法」や「含意」などと言います。
また、条件(~ならば)を規定する前の部分を「前件」、結果(ならば~)として導かれる後ろの部分を「後件」と言います。
前件(仮定、条件)を肯定することによって、後件(結果)を導くものであることから、「前件肯定」と言われます。
「PならばQ」の肯定/否定を裏返して、「notPならばnotQ(PでないならばQでない)」とすると、誤りの可能性を生じさせ、一見正しそうに見えて間違っている「前件否定の誤謬」と言う代表的な誤謬となります。
「PならばQ」の前件と後件を逆にして、「QならばP」としても誤りの可能性を生じさせ、一見正しそうに見えて間違っている「後件肯定の誤謬」と言う代表的な誤謬となります。
「PならばQ」を対偶(逆裏)の関係「notQならばnotP(QでないならばPでない)」にした場合は、正しくなり、これを「対偶の法則」と言います。
1.正・前件肯定(PならばQ)~運転免許証を取得した人ならば運転ができる。
2.裏・前件否定(notPならばnotQ)~運転免許証を取得していない人ならば運転ができない。
3.逆・後件肯定(QならばP)~運転ができるならば運転免許証を取得した人だ。
4.対偶(逆裏)・後件否定(notQならばnotP)~運転ができないならば運転免許証を取得していない人だ。
このうち正しい推論は1.4.で、誤りの可能性をもつのが2.3.です。
2.3.では無免許運転の可能性があります。
問題は、PならばQという条件文において、条件Pが満たされない場合のことは何も語られておらず未規定であるため、Qを導出する別の可能性が残るということです。
後件否定は、対偶によって命題の真偽を証明するため、「対偶論法」とも呼ばれます。
まとめると、以下のようになります。
原命題A「PならばQ」…正しい推論
Aの逆「QならばP」…誤った推論
Aの裏「notPならばnotQ」…誤った推論
Aの対偶「notQならばnotP」…正しい推論対偶の法則「PならばQ⇔notQならばnotP」
前件肯定式 ((P⇒Q)∧P)⇒Q
後件否定式 ((P⇒Q)∧¬Q)⇒¬P
この「ならば」は、いくらでも推移的につなげることが出来ます。
PならばQ、QならばR、RならばS、Sならば・・・。
これを「推移律」と言います。
「PならばQ、QならばR、よってPならばR」
形式的に書くと「<PならばQ>かつ<QならばR>ならば<PならばR>」、記号的には((P⇒Q)∧(Q⇒R))⇒(P⇒R)。
いわゆる「仮言三段論法」と呼ばれているものです。
五節、ド・モルガンの法則
論理積(連言)と論理和(選言)は、否定を介した双対の関係にあり、これを「ド・モルガンの法則」と言います。
“選言の否定”は”否定の連言”と等しくなり、”連言の否定”は”否定の選言”と等しくなる、という法則です。
1.選言の否定「<PまたはQ>ではない」⇔否定の連言「<Pでない>かつ<Qでない>」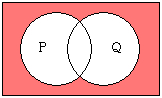
¬(P∨Q)⇔¬P∧¬Q
2.連言の否定「<PかつQ>ではない」⇔否定の選言「<Pでない>または<Qでない>」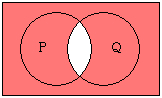
¬(P∧Q)⇔¬P∨¬Q
例1.選言の否定「<花がある、または団子がある>ではない」=否定の連言「<花がない>かつ<団子がない>」
例2.連言の否定「<花があり、かつ団子がある>ではない」=否定の選言「<花がない>または<団子がない>」
少々分かりにくいかもしれませんが、論理学における「または」とは、PとQの最低どちらか一方は成り立つ(包含的論理和)であることを思い出してください。
命題が三つ以上ある場合も同様です。
¬(P∨Q∨R)⇔¬P∧¬Q∧¬R
¬(P∧Q∧R)⇔¬P∨¬Q∨¬R
結び
以上のような、言葉のつながり(関係付け)の基本的な規則(論理の規則)の組み合わせにより、物事の真偽を損なわない論理的な思考が可能になります。
この組み合わせ(言葉のつながり)の中に、逆の推論(後件肯定の誤謬)や裏の推論(前件否定の誤謬)などが混ざると、最終的に誤った推論となってしまいます。
多くの場合、「ならば(つまり推論、演繹)」によって言葉をつなぐ時に誤謬の危険が生じてくるので、特に注意する必要があります。
