第五章、述語論理
一節、述語論理の語彙「個体と述語の記号」
述語論理は命題論理の拡張で、命題を主語と述語に分解し、より詳細に探究するものです。
命題論理の概念やシステムの土台の上に構築されます。
命題論理において「ソクラテスは人間である」は、一つの命題記号Pで表されましたが、述語論理では個体名「ソクラテス」と述語「~は人間である」に分解し、「人間である(ソクラテス)」と捉えます。
述語を任意の大文字のアルファベット、個体を小文字のアルファベットで表し、「F(a)」という形になります(個体を括弧でくくるかどうかは自由です)。
述語「人間である」を述語記号F、ソクラテスを個体記号a、プラトンをbとすると、「ソクラテスは人間である」は「Fa」、「プラトンは人間である」は「Fb」となります。
固有名で表される個体記号を「個体定項」と呼びa,b,c,などと表され、任意の変項であるものを「個体変項」と呼びx,y,z,などと表されます。
定項は数学で言う定数、変項は変数です。
数学において定数はa,b,c,…の記号がよく用いられ、変数の記号はx,y,z,…がよく用いられるため、論理学においてもそれを踏襲する研究者が多いですが、決まり事ではありません。
述語記号F,G,H,…も同様、数学における関数の記号「F(関数を意味するfunctionの略)」がよく用いられますが、決まり事ではありません。
個体定項を個体変項に変換したものを「命題関数」と呼びます。
ですから、命題関数は、個体変項と述語のみから成ります。
例えば、「ソクラテスは人間である」という命題のソクラテスを、何でも代入可能な個体変項xとして、人間であるを述語記号Fとした場合、「F(x)」がこの命題関数となります。
述語との関りを持つ個体変項xは、ある程度その存在範囲を定めた上で議論する必要があり、それを「個体領域(議論領域)」と呼びます(関数の定義域に当たるもの 2≦x≦8 みたいな)。
人間に関わる述語であれば、議論の対象(個体)を人間に限っておかなければなりません。
また、以下のように、論理式を簡略化することができます。
個体領域を定めないまま「すべての日本人は日本語が話せる」を式にすると、∀x(Fx→Gx)「すべてのxについて、xが日本人ならば、xは日本語が話せる」となります(∀xについては次節参照)。
そこで個体領域D(discourseのDが由来)を「日本人」と設定しておけば、∀xFxと簡略化できます。
ちなみに固有名でない普通名詞(日本人、猫など)は述語であり、個体定項の式Faだけで表すことは出来ません(述語論理の基礎を作ったアリストテレスは、「人間」や「猫」を個体の属性-述語-としてとらえます)。
二節、述語論理の語彙「量化する記号」
さらに個体は数量的な質「すべての~」「ある~」を扱うことが可能です。
「すべての~(for all ~)」は「All(全て)」のAの上下反転で「∀」という記号で表され、「全称量化記号、普遍量化記号 (universal quantifier) 」などと呼ばれます。
「ある~(for some ~)」は「Existieren(在る)」のEの左右反転で「∃」という記号で表され、「特称量化記号、存在量化記号 (existential quantifier)」などと呼ばれます。
述語をF、個体変項をxとした場合、「すべてのxはF」は「∀xFx」として表され、「あるxはF」は「∃xFx」として表されます。
「∀xFx」を日本語にすると、「すべてのxは、Fである」「すべてのxについて、xはFである」「どの(任意の)xもFである」などとなります。
「∃xFx」を日本語にすると、「あるxは、Fである」「あるxについて、xはFである」「Fであるxが(少なくとも一つ)存在する」などとなります。
このように量化記号∀および∃が入った命題を「量化命題」といいます。
量化子の適用範囲を量化子の作用域と呼びます。
たとえば、∀x(∃yF(x,y))の場合、∀xの作用域は(∃yF(x,y))の部分、∃yの作用域はF(x,y)の部分となります。
量化子に量化される個体変項は、作用域内の同じ文字の変項(∀xならxのみ、∀yならyのみ)です。
個体変項xが量化記号(∀x,∃x)によって量的に限定(束縛)されている時、これを「束縛変項(bound variable)」と呼び、反対になんの束縛もない個体変項は「自由変項(free variable)」と呼びます。
例えば、∀xF(x,y)の場合、xは束縛変項、yは自由変項です。
一つの命題に量化子が二つ以上入る多重量化の場合、量化子の順番とその作用域をしっかり把握しておかないと誤りが生じます。
F(x,y)を「xはyが好きである」、xの定義域を日本人、yの定義域を和食とした場合、∀x∃yFxyは「すべての日本人には、好きなある和食がある(太郎は寿司、花子は天婦羅、次郎は煮魚、…)」、∃y∀xFxyは「すべての日本人は、ある和食が好きである(太郎も花子も次郎も…日本人皆、すき焼きが好き)」という意味になります。
∀x∃yFxyという量化命題は、丁寧に書くと(∀x(∃yF(x,y))) 、∃y∀xFxyという量化命題は、(∃y(∀xF(x,y))) となり、量化子の作用域が異なっていることが分かります。
前者は、(∃yF(x,y))=「日本人にはある好きな和食がある」に対して全称量化子∀xがかかっているので、和食好きの日本人の総体を意味することになります。
後者は、(∀xF(x,y))=「すべての日本人は和食が好きである」に対し特称量化子(存在限定子)∃yがかかっているので、その和食がある特定の存在として限定されています。
三節、述語の意味
述語論理における「個体」と「述語」は私たちが日常で使う自然言語の「主語」と「述語」とは異なり、文法的主語が個体とは限らず文法的述語が述語論理的述語とは限りません。
述語論理における述語とは、あくまで個体の性質や関係を表すもので、一項述語はその一つの個体の性質を表し、二項(以上の)述語は二つの個体の間の関係を述べるものです。
個体がが二項以上のものを多項述語と呼び、二つの場合はF(a,b)、三つの場合はF(a,b,c) 、n個のn項述語の場合はF(a1,a2,…,an)と記します。
F(a)は「aは性質Fをもつ」ということであり、例えば、aを「ソクラテス」、Fを「~は人間である」とした「ソクラテスは人間である」というような命題です。[個体と述語の関係の詳細は、アリストテレスの頁をご覧ください]
F(a,b) は「aとbはFの関係にある」ということであり、aを「プラトン」bを「ソクラテス」、Fを「~は~を愛している」とした「プラトンはソクラテスを愛している」というような命題です。
F(b,a)であれば、「ソクラテスはプラトンを愛している」となります。
述語論理で使用する語彙、及び記号のまとめ
個体定項:a,b,c,…(固有名をもつ個体)
個体変項:x,y,z,…(一般的個体)
述語:F,G,H,…(各項-個体-を関係付ける関数)
論理記号:¬,∧,∨,⇒,⇔(否定、論理積、論理和、含意、同値)
量化子:∀,∃(全体、部分)個体領域(個体変項の範囲、定義域):D
※基本的に命題論理と同じです。命題論理の命題Pが、個体と述語と量化子に分かれ、詳細に表されたものです。
※括弧の略記…前頁の命題論理の時と同様、論理式における括弧()は、記号と命題の結び付きの強さに応じ、式の意味が変わらない限りで省略可能です。命題(項+述語の事)と最も強く結びつく記号が¬,∀,∃、次いで∧, ∨、次いで⇒,⇔となります。
四節、量化命題の否定(ド・モルガンの法則)
命題論理において連言と選言が否定を介した双対の関係にあることを指した「ド・モルガンの法則」は、全称命題と存在(特称)命題においても機能しています。
「全称の否定は否定の特称、特称の否定は否定の全称」であり、以下のようになります。
全称肯定命題∀xFx「すべてのxはFである」
全称否定命題∀x¬Fx「すべてのxはFでない」
特称肯定命題∃xFx「あるxはFである」
特称否定命題∃x¬Fx「あるxはFでない」全称肯定命題の否定=特称否定命題
¬(∀xFx)=∃x¬Fx
(すべてのxはFである)でない=あるxはFでない
“すべての人間は死ぬ”の否定=ある人間は死なない
[xの個体領域を「人間」、述語Fを「死ぬものである」とした場合。ちなみに否定が全体にかかっている¬(∀xFx)ので、述語だけでなく量化子もひっくり返す必要があります。”すべて(全体)”は”ある(部分)”に、”死ぬ”は”死なない”に変換。]全称否定命題の否定=特称肯定命題
¬(∀x¬Fx)=∃xFx
(すべてのxはFでない)でない=あるxはFである
“すべての人間は死なない”の否定=ある人間は死ぬ特称肯定命題の否定=全称否定命題
¬(∃xFx)=∀x¬Fx
(あるxはFである)でない=すべてのxはFでない
“ある人間は死ぬ”の否定=すべての人間は死なない特称否定命題の否定=全称肯定命題
¬(∃x¬Fx)=∀xFx
(あるxはFでない)でない=すべてのxはFである
“ある人間は死なない”の否定=すべての人間は死ぬ
量化命題の選言と連言の否定の関係も、以下のように双対の関係になります。
¬(∀x(Fx∧Gx))=∃x(¬Fx∨¬Gx)
¬(∀x(Fx∨Gx))=∃x(¬Fx∧¬Gx)
¬(∃x(Fx∧Gx))=∀x(¬Fx∨¬Gx)
¬(∃x(Fx∨Gx))=∀x(¬Fx∧¬Gx)
例えば、一段目¬(∀x(Fx∧Gx))の否定は全体にかかっているので、∀xの否定は=∃x、(Fx∧Gx)の否定はド・モルガンの法則に従い=(¬Fx∨¬Gx)となり、∃x(¬Fx∨¬Gx)と同値であることが分かります。
五節、述語論理の意味論
命題論理の意味論においては、単純に真1と偽0の二値だけを考えればよかったのですが、述語論理においては、命題が個体と述語と量化子に分かれているので、命題の真偽を問う前にその命題の論理式の内容を明確にするために以下の作業が必要になります。
1.述語記号に具体的な意味を充てる
2.個体定項に具体的な意味を充てる
3.個体領域D(個体変項の定義域)を具体的に定める
このように、論理式に具体的な意味を充てる作業を述語論理における「解釈」といいます。
全称量化命題∀xFxが真であるとは、個体領域Dに属する任意(全て)の個体において、述語Fで述べられていることが真である時です。
特称(存在)量化命題∃xFxが真であるとは、個体領域Dに属するある(少なくとも一つの)個体において、述語Fで述べられていることが真である時です。
例えば、個体領域Dを「京都人」、述語Fxを「xは意地悪である」を充てると、∀xFxは「すべての京都人は意地悪である」と解釈されます。
吉岡里帆も中村玉緒も意地悪ではないので、「個体領域Dに属する任意(全て)の個体が真である時」が成立せず、この命題は「偽」となります。
個体領域を「シンデレラの継母家族」とすれば、全員意地悪なので、この命題は「真」となります。
六節、述語論理の構文論
述語論理における論理式には、(上の例のような)1.解釈によって真偽が分かれる論理式、2.いかなる解釈でも真となる論理式、3.いかなる解釈でも偽となる論理式、の3パターンがあります。
命題論理において、命題がいかなる真理値を取ろうとも恒に真である論理式を「恒真式」と呼びましたが、述語論理においては、命題がいかなる解釈(定項、述語、個体領域)を取ろうとも恒に真である論理式を「妥当式」と呼びます(上の2.)。
命題論理において恒真式であるかどうかは、真理表の作成によって機械的に決定することができましたが、述語論理では、この手続きが使えないため、構文論的方法による証明が有効に成ってきます。
証明における基本的な手続きは命題論理と変わらず、命題論理の推論規則に量化子の四つの推論規則を加えたものが用いられます。
規則1「全称の導入則(全称汎化)」…Fu(任意の個体u)から∀xFxを導出できる。[∀I]
Fu⇒∀xFx
任意の個体がFならば、すべての個体xについてFである。規則2「全称の除去則(全称例化)」…∀xFxからFa(特定の個体a)あるいはFu(任意の個体u)を導出できる。[∀E]
∀xFx⇒Fa、∀xFx⇒Fu
すべての個体xについてxがFならば、特定の個体aはF、あるいは任意の個体uはFである。規則3「存在の導入則(存在汎化)」…Faから∃xFxを導出できる。Fuから∃xFxを導出できる。[∃I]
Fa⇒∃xFx、Fu⇒∃xFx
特定の個体aがF、あるいは任意の個体uがFならば、あるxについてFである。規則4「存在の除去則(存在例化)」…∃xFxからFaが導出できる。[∃E]
∃xFx⇒Fa
あるxについてxがFならば、特定の個体aはFである。
例えば、アリストテレスの有名な三段論法を証明する場合は、以下のようになります。
Fx=xは人間である
Gx=xは死すべきものである
a=ソクラテス
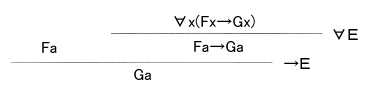
全ての人間は死すべきものである ∀x(Fx⇒Gx)
ソクラテスは人間である Fa
よって、ソクラテスは死すべきものである Ga
1 ∀x(Fx⇒Gx) [前提]
2 Fa [前提]
3 Fa⇒Ga [1をaで全称例化∀E]
4 Ga [2,3より]
おわり
【おすすめの本】
『例解 論理学入門』弓削隆一/佐々木昭則著、ミネルヴァ書房
『論理学』野矢茂樹著、東京大学出版会
『論理学』大西琢朗著、昭和堂
『まったくゼロからの論理学』野矢茂樹著、岩波書店
上から順に、慶應、東大、京大の論理学入門の講義内容をベースにしたものです。
四冊目は、中高生や一般層をターゲットにしたもので、最初の一冊に最適です。

